Roberto Rampini
Il Sistema temperato inequabile ‘Rampini III’
(2016)

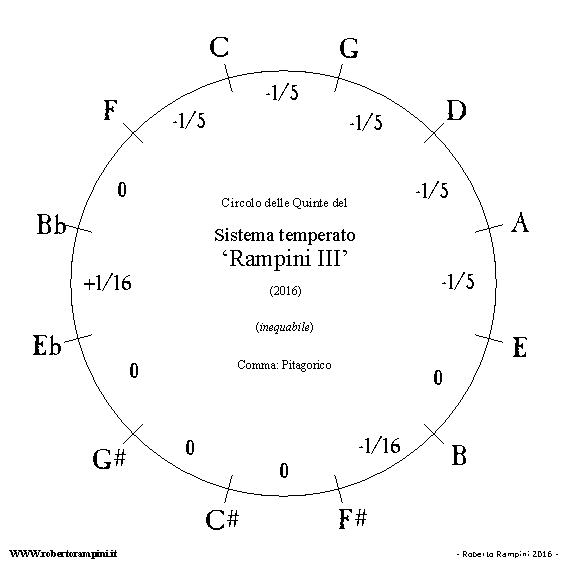
Fig.1: Circolo delle Quinte del sistema 'Rampini III'
Introduzione
Nel luglio 2016 ho realizzato i mie due primi ‘temperamenti inequabili’ (‘Rampini I’ e ‘Rampini II’) per strumenti a tastiera, da me definiti di tipo ‘simmetrico’ poiché entrambi i sistemi si allontanavano per l’appunto in modo simmetrico e progressivo dalla terza naturale di Do maggiore con l’aumento dei numeri di diesis o bemolli in chiave (ovvio criterio di base seguito anche nei secoli scorsi, ma a mio parere in modo non sufficientemente sistematico e con risultati spesso approssimativi).
Il presente tentativo, da me compiuto allo scopo di creare un temperamento che partisse da ben due terze prossime all’intervallo naturale (anziché una sola) mi ha inevitabilmentre ricondotto ad alcuni sistemi di origine tedesca già formulati nel passato (e ripresi anche in epoca recente da studiosi quali ad esempio Herbert Anton Kellner, nel 1975), caratterizzati da cinque intervalli di quinta che vengono diminuiti di 1/5 di comma pitagorico (più altri eventuali ‘aggiustamenti’ secondari fatti allo scopo di evitare la presenza di troppi intervalli di terza maggiore che superino l’intervallo pitagorico di 81/64).
Mi riferisco qui in particolare al sistema di accordatura ‘Bach/Swich’ (così definito dall’australiano Carey Beebe nel suo Sito Internet CBH): è questo un temperamento inequabile che sembra sia stato adottato dallo stesso J.S.Bach, secondo la suggestiva ipotesi avanzata per primo nel 2005 dallo statunitense Bradley Lehman: nel criptico disegno ‘ornamentale’ che compare sul frontespizio del Clavicembalo ben temperato le ‘volute grafiche’ manoscritte corrisponderebbero infatti a precise ‘correzioni delle quinte’ (da applicare poi nell’accordatura dello strumento).
Pur accorgendomi presto che rispettare anche in questo mio studio la perfetta simmetria adottata nei miei primi due temperamenti (con il vincolo delle due terze naturali di partenza) si rivelava un’impresa irrealizzabile dal punto di vista matematico, l’inevitabile rinuncia ai miei iniziali propositi ’simmetrici’ mi ha però poi condotto, e con mia grossa sorpresa, ad ottenere un originale e valido temperamento inequabile simile al ‘Bach/Swich’ ma che, al suo confronto, offre un paio di non disprezzabili vantaggi:
1) Nel mio ‘Rampini III’, a motivo delle sue ben cinque quinte pure (a differenza delle solo tre presenti nel ‘B/S’) , l’accordatura secondo la prassi tradizionale risulta ancor più facile e immediata.
2) I due intervalli di terza maggiore più ‘critici’ presenti nel ‘B/S’ (poiché superiori all’intervallo di terza pitagorica: Do#/Mi# e Fa#/La#, pari a 409,8 Cent) presentano entrambi nel ‘R-III’ un valore più ridotto (409,3 Cent).
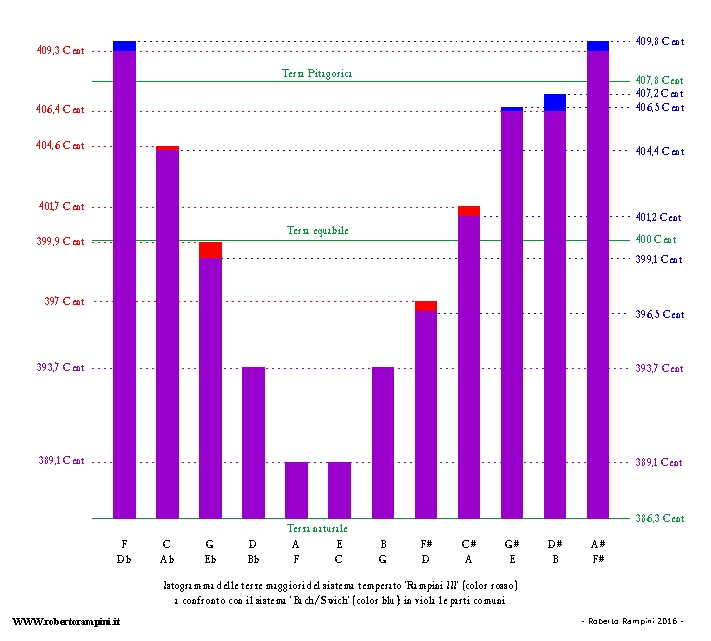
Fig.2: Istogrammi delle terze maggiori nel 'Rampini III'
(in rosso)
e
nel 'Bach/Swich' (in blu): in viola le parti comuni ai due sistemi.
Caratteristiche del Sistema
Per quanto riguarda le terze maggiori il mio sistema offre otto differenti ordini di ‘grandezza’: due terze vicine al valore naturale (Fa/La e Do/Mi), due terze naturali crescenti (SIb/Re e Sol/Si), una terza ben al di sotto al valore equabile (Re/Fa#), una terza quasi equabile (Mib/Sol), due diverse terze equabili crescenti (La/Do# e Lab/Do), due terze di valore inferiore a quello pitagorico (Mi/Sol# e Si/Re#) e infine due terze pitagoriche leggermente crescenti (Reb/Fa e Fa#/La#). Invito in proposito ad esaminare l’utile istogramma di fig. 2, nel quale metto a confronto le terze del mio sistema (di color rosso) con quelle del ‘B/S’ (di color blu); in viola sono invece riportati gli elementi comuni ai due sistemi.
Per le quinte abbiamo invece cinque intervalli ‘puri’ (Mi/Si , Fa#/Do#, Do#/Sol#, Lab/Mib e Sib/Fa), cinque quinte in sequenza più ‘strette’ di 1/5 di comma pitagorico (Fa/Do, Do/Sol, Sol/Re, Re/La e La/Mi) una quinta calante di 1/16 di comma pitagorico (Si/Fa#) ed infine l’unica quinta ‘crescente’ del sistema (Mib/Sib), anch’essa temperata di 1/16 di comma: da notare l’elegante e complessiva disposizione ‘simmetrica’ dei valori che ne risulta, con due opposti intervalli corretti della stessa misura (ma di segno contrario).
Il grafico di Fig.3 riporta infine le grandezze degli intervalli di semitono del sistema così impostato, con i relativi ‘scostamenti’ dal valore medio del semitono equabile (100 Cent), passando da un minimo di -11,2 Cent (Fa/Fa#) ad un massimo di + 13,7 Cent (Mi/Fa).
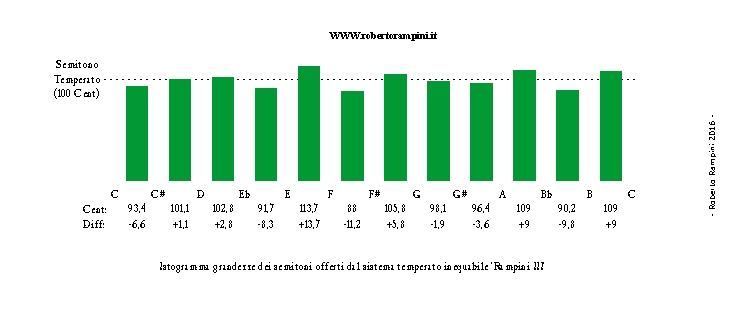
Fig.3: Istogrammi dei semitoni nel sistema 'Rampini III'
Per provare in pratica questo sistema senza servirsi di apparecchiature elettroniche basterà anzitutto accordare in ‘senso orario’ cinque quinte diminuite di 1/5 di comma pitagorico (da Fa a Mi), accordare la quinta pura Mi/Si per poi temperare la quinta Si/Fa# diminuendola di 1/16 di comma pitagorico ed infine procedere all’accordatura di tre quinte pure in sequenza (Fa#/Do#, Do#/Sol#, LabMib) nonché dell’isolata e restante quinta pura Sib/Fa. Se le suddette operazioni saranno tutte realizzate in modo corretto anche l’ultima quinta Mib/Sib (crescente di 1/16 di comma) risulterà opportunamente accordata.
Per chi invece volesse sperimentare in pratica sul suo strumento gli effetti sonori di questo sistema con l’ausilio di un frequenzimetro potrà servirsi di una delle tabelle di
figg.4-6 (facilmente ottenute con il mio programma ‘the Well-Tempered Software’), che riportano tutti i valori in Hertz delle frequenze di ciascuna nota (precise fino a quattro decimali arrotondabili a piacere): la prima tabella elenca le frequenze del Sistema con l’attuale diapason a 440 Hz, la seconda e la terza con diapason più bassi (rispettivamente 430 e 415 Hz), senz’altro più adatti per strumenti ‘d’epoca’ (spinette e clavicembali non progettati per sopportare forti tensioni d’accordatura).
Se qualcuno desiderasse poi provare il temperamento proposto con altri diapason, non ha che da scrivermi all’indirizzo
robertorampini57@gmail.com e sarò ben lieto di fornirgli una tabella su misura delle sue esigenze.
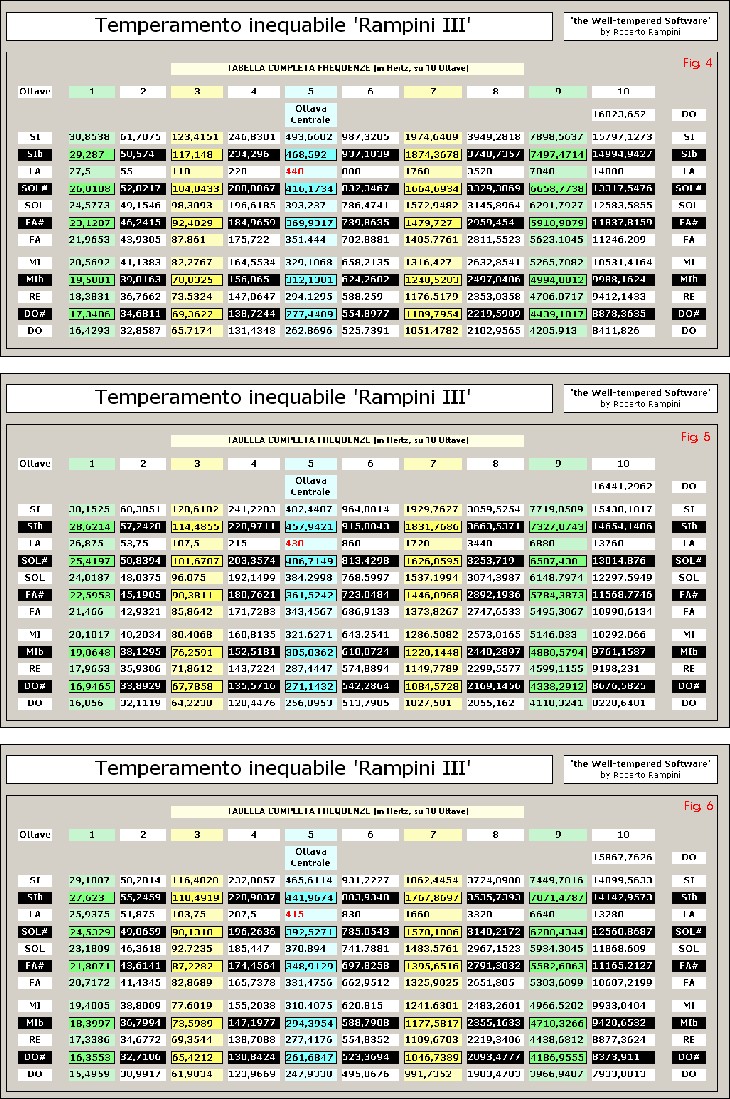
Figg.4-6: Tabelle frequenze per il sistema inequabile 'Rampini III'
![]() Download 'Rampini III - Temperamento inequabile 2016.pdf
(3,5 Mb)
Download 'Rampini III - Temperamento inequabile 2016.pdf
(3,5 Mb)
- © Roberto Rampini 2016 -
Proprietà dell’Autore
- Tutti i diritti riservati -
WWW.robertorampini.it